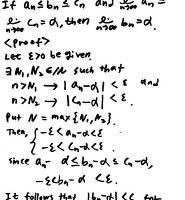| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 옥스포드 라틴 코스
- 옥스포드 라틴어
- 독일
- 수학올림피아드
- New York Excelsior
- 샌드위치 정리
- NY Excelsior
- 수학
- sandwich theorem
- 라틴어 비교급
- 세계사
- 역사
- 봉건제
- 해석학
- 정수론
- 피렌느
- 7의 배수
- 라틴어 해석
- 악법
- 오버워치 리그
- 유럽사
- 서양사
- sqeeze theorem
- 라틴어 문법
- RSA 알고리즘
- 라틴어
- 다이모니온
- 배수 판정법
- 중세사
- 조임 정리
- Today
- Total
친절한 공대생
RSA 알고리즘: 수학으로 내 돈을 지키다 (1. 암호론편) 본문
한 수학 난제가 해결되면 당신의 계좌가 뚫린다?
자그마치 11억원의 상금이 걸려있는 수학 난제, '리만 가설'의 해결을 앞둔 수학자의 딸이 납치된다. 납치범들이 요구하는 것은 리만 가설의 해답. 납치범들의 목표는 소수의 규칙성을 설명하는 리만 가설을 풀어서 전 세계의 보안 프로그램을 뚫는 것이다.1
위 내용은 미국 드라마 「Numbers」의 한 에피소드이다. 이 드라마를 보고 당신의 계좌가 덜컥 불안해지는가? 사실 리만 가설이 해결되더라고 당신 계좌가 뚫릴 일은 없다. 하지만 소수가 인류의 보안을 책임지고 있다는 것은 사실이다. 그래 그래. 이해한다. 중학교 때 배운 그 소수가 보안이랑 무슨 상관이냐고 따지고 싶을 것이다. 그 이유를 이해하려면 기초적인 암호론과 정수론을 알아야한다. 골아픈 수학이 어떻게 내 돈을 지켜주고 있는지 알아보자.
대칭키 암호: 둘만의 암호를 만들자!
우리는 소중한 정보를 타인에게 들키지 않고 상대방에게 알려주기 위하여 원래의 정보를 암호화한다. 그리고 수신자는 자신이 받은 암호를 원래의 형태로 바꾸기 위하여 암호를 푼다. 그것을 복호화라고 한다.
실제로 역사적으로 사용되었던 암호를 통해 얘기를 계속 해나가겠다. 지금부터 소개할 것은 로마의 군인인 율리우스 시저가 군사 기밀을 보호하기 위해 사용했던 시저암호이다. 당신이 독립군이라고 가정하자. 당신은 검을 대걸레로 위장하여 보관해두었다. 동지에게 검이 있는 위치를 알려주기 위하여 당신은 그에게 '대걸레(MOP)'를 암호화하여 쪽지를 전해주고 싶다. 그래서 당신은 각 알파벳을 알파벳 순서로 세 칸씩 밀기로 하였다. 'a'는 'd'로, 'b'는 'e'로, ..., 'z'는 'c'로 교체되는 것이다. 그럼 원문 'MOP'은 다음과 같이 암호화된다.
복호화는 암호문의 알파벳을 암호화할 때 앞으로 민 횟수만큼 다시 뒤로 당기면 된다. 'd'는 'a'로, 'e'는 'b'로 ... 이런 식이다. 따라서 암호를 받은 동지는 암호문 'PRS'를 다음과 같이 복호화한다.
그런데 당신은 시저 암호의 방식을 여전히 사용하면서도 알파벳을 밀고 당기는 횟수를 바꿀 수 있다. 원문 'MOP'를 암호화할 때 알파벳을 두 번 밀면 암호는 'OQR'이 되고, 네 번 밀면 'QST'가 된다. 즉, 당신은 암호를 만드는 방법은 유지하면서 알파벳을 미는 횟수를 바꾸어 하나의 원문을 서로 다르게 암호화할 수 있다. 이 때 바뀌지 않는 암호화 체계를 '암호화 알고리즘'이라고 부르고, 암호화할 때마다 바꿀 수 있어서 암호 결과를 바꾸는 일련의 정보를 '키(Key)'라고 부른다. 당신이 사용한 암호화 알고리즘은 '시저 암호 방식'이고 키는 '3'이다. 왜냐하면 당신은 알파벳을 세 번 밀고 당겼기 때문이다. 만약 알파벳을 두 번 밀고 당기기로 약속했다면 키는 2가 되고, 다섯 번으로 약속했다면 키는 5가 된다.
요약하자면, 암호를 만들기 위해서는 1. 어떤 암호화 알고리즘을 쓸 것인가 2. 키를 무엇으로 정할 것인가. 이 두 가지를 정해야한다. 아래 그림은 f라는 암호화 알고리즘을 선택했을 때 암호화와 복호화를 도식으로 표현한 것이다.
한편, 시저암호에는 우리가 주목해야할 점이 하나 있다. 잘 보면 알겠지만, 암호를 만들고 풀 때 사용하는 키가 같다! 암호화할 때 알파벳을 N번 밀었다면, 복호화할 때도 알파벳을 N번 당기게 된다. N이라는 하나의 키로 암호화와 복호화를 모두 할 수 있는 것이다. 이렇게 암호화와 복호화에 사용되는 키가 같은 암호화 알고리즘을 대칭키 암호라고 한다. 인류가 기원전부터 1900년대 초반까지 써왔던 모든 암호는 대칭키 암호에 속한다.
대칭키 암호의 허점
이제는 독립군이 2명이 아니라 8명이라고 하자. 이들이 대칭키 암호 방식을 사용해서 서로 통신한다면 어떤 일이 벌어질까?
일단 모두가 같은 키를 사용해서 암호를 교환하는 경우를 생각해보자. 독립군 A가 독립군 B에게 폭탄 투척 대상을 암호화해서 쪽지에 적어 보냈다. 그런데 동지인줄만 알았던 스파이 C가 그 쪽지를 가로챘다! 모두가 같은 키를 사용하고 있기 때문에 C는 A가 암호화할 때 사용했던 키를 알고 있다. 대칭키 암호 체계에서는 암호화할 때 사용한 키를 통해서 복호화가 가능하므로 C는 A의 암호를 쉽게 해독할 수 있다. 이렇게 쉽게 독립군의 폭탄 투척 대상은 일본의 정보통으로 들어가버리고 만다...
그럼 '도청'을 막기 위해서 어떻게 해야할까? 어느 독립군이 또다른 독립군과 소통할 때 쓰는 키를 그 둘 외에는 누구도 몰라야하므로 각 쌍마다 서로 다른 키가 주어져야할 것이다. 8명의 독립군을 두 명씩 짝지었을 때 어떤 일이 벌어지는지 도식으로 나타내었다.
보시다시피 아주 많은 키가 필요하다. 정확하게는 8 × 7 ÷ 2 = 28 쌍이다. 즉, 8명이 쌍을 이루어 각자 키를 가지게 된다면 28개의 서로 다른 키가 필요한 것이다. 이 개수는 사람이 늘어날 수록 급격하게 커져 20명이면 190개, 50명이면 1225개가 필요하다. 수학적으로는 n명의 사람이 있을 때 필요한 키의 개수는 개가 된다. 2
즉, 대칭키 암호 체계는 1. 같은 키를 사용해 도청이 가능하거나 2. 도청을 막기 위해 너무 많은 키가 필요하거나. 두 허점이 있다.
공개키 암호: 암호계의 새로운 패러다임
인류가 2000년동안 머물러있던 대칭키 암호 패러다임은 1976년 디피와 헬만에 의해서 깨부수어진다. 그들은 암호화할 때 필요한 키와 복호화할 때 필요한 키가 서로 다른 암호화 알고리즘을 개발한다. 그것을 '공개키 암호'라고 부른다. 공개키 암호 체계에서는 두 종류의 키가 존재한다. 하나는 모두가 알 수 있는 공개키이고, 다른 하나는 권한을 가진 소수만 알 수 있는 비밀키이다. 공개키는 암호화할 때 필요하다. 따라서 암호화 자체는 이미 알려진 공개키를 이용해서 누구나 할 수 있다. 하지만 공개키로 복호화를 하려면 몇 억년이 걸릴 정도로 오래 걸린다. 효율적으로 복호화를 하기 위해서는 비밀키가 필요하다.
공개키 암호는 마치 우체통에 비유될 수 있다. 편지를 넣는 것은 우체통의 위치만 안다면 누구든 할 수 있다. 하지만 그 안의 내용물을 열어 편지를 읽는 것은 우체통의 열쇠를 가진 자만이 할 수 있다. 우체통의 위치가 공개키의 비유이고, 우체통의 열쇠가 비밀키의 비유이다.
공개키 암호는 수신자가 한 명(혹은 한 단체)일 때 특히 유용하다. 조직의 장에게 조직원들이 암호를 보낼 때, 은행 기관이 많은 사람에게 개인 정보를 받을 때 등이 그 경우에 속한다. 어느 조직원이 조직장에게 보낸 암호를 누군가가 가로채더라도 그는 그 암호를 해독하지 못 한다. 왜냐하면 그는 공개키만 알고 있는데 공개키로 암호문을 해독하는 것은 불가능에 가까울 정도로 어렵기 때문이다.
소수를 통해 우리의 정보를 보호하는 방법(RSA 알고리즘)도 공개키 암호에 속한다. 매우 큰 두 소수를 선택한 다음, 그 두 소수를 곱한다. 그럼 어마어마하게 큰 수가 나올올 것이다. 그 수만 보고 그 수가 어떤 소수를 곱해서 만들어졌는지 알아내는 것은 시간이 매우 오래 걸린다. 작은 수로 예를 들어 보자면, 두 소수인 67과 73을 곱하면 4891이 나오는데 4891만 보고 이 수를 다시 67과 73으로 쪼개는 것은 시간이 오래 걸린다는 뜻이다. 우리가 알아보고자 하는 암호화 알고리즘은 두 소수와 관련된 것을 비밀키로 잡고, 그 두 수를 곱해져 나온 수와 관련된 것을 공개키로 잡는다. 그렇게 하여 공개키를 아는 사람이 쉽게 비밀키를 알아낼 수 없도록 만드는 것이다. 그 방법의 절차는 2탄, 정수론 편에서 설명해주겠다.
- 소수란 약수가 1과 자가 자신뿐인 2 이상의 자연수를 의미한다. 6은 약수가 1,2,3,6인데 2와 3은 1도 자기 자신도 아니다. 따라서 6은 소수가 아니다. 하지만 7은 약수가 1, 7 뿐이다. 따라서 7은 소수이다. 그 외에도 소수에는 2,3,5,11,13 등이 있다. 1은 정의에 의하여 소수가 아니다. 소수는 무한히 많이 존재함이 널리 알려져있다. [본문으로]
- 한 사람이 짝을 맺을 수 있는 상대는 n명의 사람 중 자기 자신을 제외한 (n-1)명이다 총 n명이 모두 그러하므로 n(n-1)쌍이 나온다. 하지만 한 쌍이 두 번씩 중복되어 세어지기 때문에 2를 나누어 위와 같은 수식이 나오는 것이다. [본문으로]
'수학 이야기' 카테고리의 다른 글
| 극한에서의 샌드위치 정리(조임 정리) 증명 (0) | 2018.03.16 |
|---|---|
| 7의 배수 판정법과 그의 증명 (2) | 2018.03.09 |