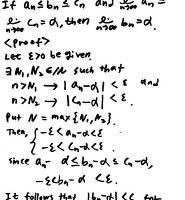| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- RSA 알고리즘
- NY Excelsior
- 유럽사
- 정수론
- 피렌느
- 배수 판정법
- 세계사
- 서양사
- 해석학
- 악법
- 라틴어 비교급
- 조임 정리
- 독일
- New York Excelsior
- 라틴어 문법
- sandwich theorem
- 봉건제
- 라틴어 해석
- 라틴어
- 옥스포드 라틴어
- 역사
- 수학올림피아드
- 샌드위치 정리
- sqeeze theorem
- 수학
- 7의 배수
- 옥스포드 라틴 코스
- 중세사
- 다이모니온
- 오버워치 리그
Archives
- Today
- Total
친절한 공대생
7의 배수 판정법과 그의 증명 본문
오랜만에 포스팅합니다. 7의 배수 판정법에 대한 유투브 동영상을 업로드했습니다. 이 블로그에는 그와 별개로 formal한 증명을 업로드해봅니다. 아래 사진이 그 증명이고, 동영상은 유투브로 설명해놓은 것입니다!
어떤 자연수가 7의 배수인지 판별하는 방법은 다음과 같습니다. 예를 들어 26069가 7의 배수인지를 판별해보겠습니다.
1. 자연수를 일의 자리 수와 그 앞의 수로 분리한다.
ex) 26069를 9와 2606으로 분리한다. 여기서 9가 일의 자리 수이고 2606이 그 앞의 수이다.
2. 1단계에서 분리한 "일의 자리 수"에 2를 곱하고, 그 수를 "그 앞의 수"에서 뺀다.
ex) 2606 - 2 * 9 = 2606 - 18 = 2588
3. 앞선 두 과정을 수가 적당히 작아질 때까지 반복한다.
ex) 258 - 2 * 8 = 258 - 16 = 242
24 - 2 * 2 = 20
4. 그 작아진 수가 7의 배수인지 여부와 원래의 수가 7의 배수인지 여부가 동일하다.
ex) 20은 7로 나누어떨어지지 않으므로 26069도 7의 배수가 아니다.
물론 1단계와 2단계를 몇 번 거치든 상관이 없습니다. 한 번 하든 열 번 하든 관계없죠. 수가 적당히 작아지기만 하면 됩니다. 1단계와 2단계를 한 번 시행하면 수는 작아지지만 그때마다 작아진 수가 원래의 수와 7의 배수 여부가 동일하기 때문입니다.
이제 이 알고리즘이 왜 성립하는지 설명하겠습니다.
1단계에서 어떤 수를 일의 자리 수와 그 앞의 수, 두 개로 분리하는 것을 수학적으로 어떻게 표현할까요?
일의 자리 수를 n으로, 그 앞의 수를 m으로 표기하면, 분리되기 전의 큰 수는 10m + n 으로 표현됩니다.
m에 10을 곱하는 이유는 우리가 수를 표기하는 방법이 십진법이기 때문이죠.
2단계에서 우리는 어떤 수를 10m + n 의 형태로 본 다음 그 m과 n으로 m-2n이라는 새로운 수를 만듭니다.
4단계에서 말하는 바는, 10m + n과 m-2n이 7로 나눈 나머지가 같다는 것이죠.
그 사실은 다음과 같은 항등식을 통해 알 수 있습니다.
m - 2n = 7*(3m) - 2(10m + n)
10m + n = 7*(3n) + 10(m - 2n)
참고) W.T.S는 Want To Show의 약자입니다. 제가 악필이라 n과 7이 비슷하게 보이니 알아서 잘 구분해서 읽으시길 ㅎ
'수학 이야기' 카테고리의 다른 글
| 극한에서의 샌드위치 정리(조임 정리) 증명 (0) | 2018.03.16 |
|---|---|
| RSA 알고리즘: 수학으로 내 돈을 지키다 (1. 암호론편) (0) | 2017.08.15 |
Comments